Clase ----------> 1 de Novimbre

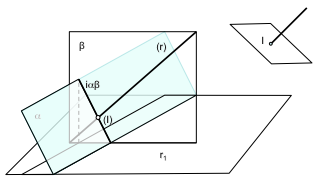
Recta determinada por dos planos.
La rectas entre dos puntos se da por  la intersección de dos planos se generando una recta  que se representa de manera matemática :

Los vectores normales serán:

El productos cruz entre estos dos vectores se obtiene un vector perpendicular a dichos vectores y este sera el vector director de la recta que se quiere calcular, obteniendo:

PARA X=0

 ecuaciones canónicas de la recta 

Ecuacion dela recta de la interseccion de dos planos

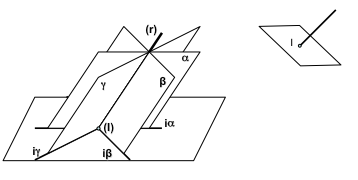
 Ecuación de un haz de planos.

                                    

Dividiendo toda la ecuación para alfa se obtiene:

El vector normal de esta haz de planos 

Haz de planos

Como se sabe todo plano puede rotar en un eje fijo, si se toma una recta,se obtendra  infinitos planos que se pueden intersecar en la misma curva. 

Mediante la ecuaciones generales se puede deducir una ecuación general para el haz de planos formado

Distancia de un punto a plano 

ECUACIÓN VECTORIAL DE LA ESFERA 

Ecuación de la esfera (centrada en el origen O): siendo R el radio de la esfera centrada en el origen.

Ecuación de la esfera centrada en un punto 

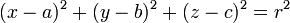
Bibliografia

http://www.ehu.eus/juancarlos.gorostizaga/apoyo/geometr1.htm

http://www.vitutor.com/geo/rec/e_12.html

http://geomanalitica.blogspot.es/3