Laplaciano
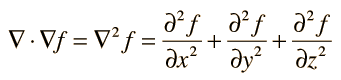
El Laplaciano encuentra aplicación en la Ecuacion de Schodinger en mecánica cuántica.
El Laplaciano, Varias Coordenadas
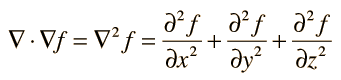
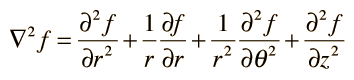
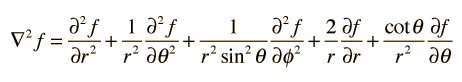
Integral de Línea
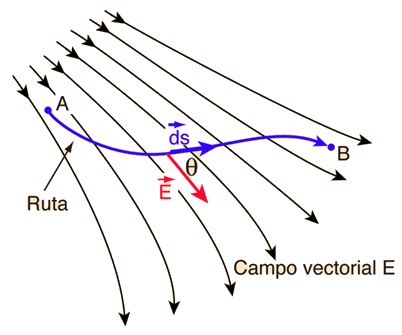 | Se dan funciones vectoriales en aplicaciones físicas tales como campo eléctrico y campo magnético. Aparecen con regularidad los productos escalares de estas funciones vectoriales, con otro vector tal como la distancia o longitud de un trayecto. Cuando tal producto se suma sobre una longitud de trayecto, donde cambian tanto las magnitudes como las direcciones, esa suma viene a ser una integral llamada integral de línea.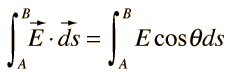 También se usa una integral de línea en la definición general de trabajo en mecánica. |
Aplicaciones de la Integral de Línea
La integral de línea del campo eléctrico alrededor de un bucle cerrado es igual al voltaje generado en ese bucle (ley de Faraday):

Tal integral se usa también en el cálculo de la diferencia de voltaje, puesto que el voltaje es trabajo por unidad de carga. El cálculo del voltaje cerca de una carga puntual es un buen ejemplo.
La integral de línea de una fuerza sobre un trayecto es igual al trabajo realizado por esa fuerza sobre el trayecto.
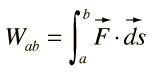
No hay comentarios:
Publicar un comentario